被概率冲昏的头脑~~~
我们先将样例在图上画下来:
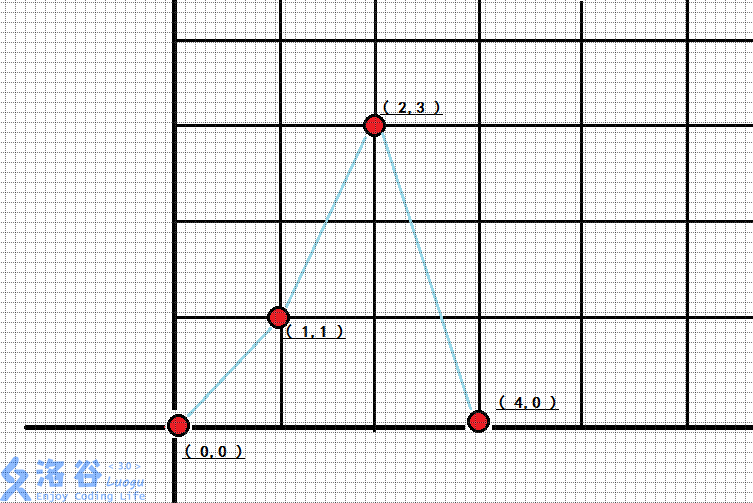
会发现,最大收益是:
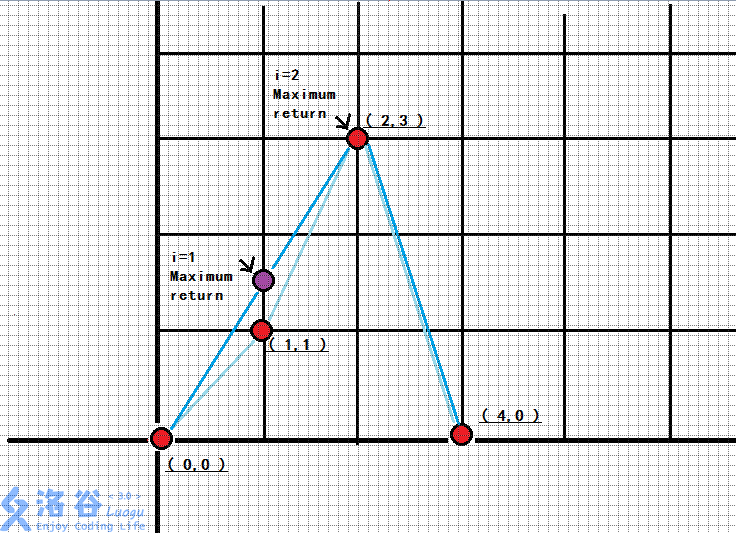 )
)
看出什么了吗?
这不就是凸包吗?
跑一遍凸包就好了呀,这些点中,如果i号点是凸包上的点,那么它的ans就是自己(第二个点),不然的话,从上图来看,i的ans肯定和他相邻的两个是凸包边界的点有关(0节点和2节点),那么怎么求这个ans呢?(第x号点为横坐标为x的点)
实际上我也不知道就是个期望公式啊!
l[i]记录i号点往左走第一个为凸包边界的点(如果i为1号,那么l[i]为0,特殊的,如果i为2号,那么l[i]就是本身),r[i]同理。当l[x]==r[x]时,x时边界。
就是这个方程: (f[l[i]])*(r[i]-i)+f[r[i]]*(i-l[i])))/(r[i]-l[i]);
基础的期望方程,在此不再赘述(实际上是不会证)
关于凸包,在这贴一波yyb大神的博客:传送门戳我QwQ(顺便膜一波yyb大神%%%)
1 |
|
本文标题:【题解】 [USACO18DEC]Balance Beam 期望+凸包 洛谷P5155
文章作者:Qiuly
发布时间:2019年02月14日 - 00:00
最后更新:2019年04月28日 - 22:20
原始链接:http://qiulyblog.github.io/2019/02/14/[题解]luoguP5155/
许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。